Steven Leinwand has a huge influence on how I approach a math lesson.  In my experience, one of the easiest ways math can be extrapolated from almost any task is by asking the questions:  How big? How far? and How Much?

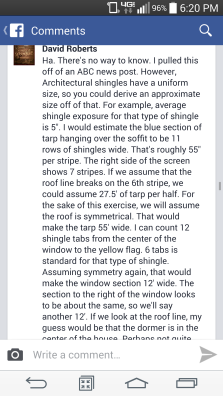
This weekend, I came across this picture on social media, posted by David Roberts:

Of course the question I asked first was “How big is that tarp!?”

Luckily, David was willing to make an estimate and allowed me to share his reasoning:

I thought it might be interesting to present the photo to my first hour and see what questions they would ask about the photo.  Of course, the surface area of the tarp was on their list.

The original article including the photo added more depth to their questions.  As it turns out, the house is being fumigated after a spider infestation.  It seems as though their curiosity surrounded more the spiders than the tarp and legitimately so.  (The article estimates the house was infested with approximately 5,000 spiders)

I was pleased that my students used visual cues in the photo to make their estimates including the average height of a story of a house, the approximate height of the man in the photo, and the size of the window.  Luckily, we found another photo that gave us a better understanding of how much tarp was needed for the other side of the house.

I’m glad this man’s golf game was not disturbed by a spider problem in the distance.  (sarcasm)

Anyway, after making some calculations, my industrial-minded first hour realized that this type of tarp must have a somewhat standard size.  After doing some Google searching and actually calling one of the companies that manufactures these behemoth plastic coverings (authentic!  Yes!), they decided that there were four 84′ x 25′ tarps covering the house and the space surrounding it. (We were able to have a nice conversation about how multiplying each dimension by 4 was different that multiplying the area of the tarp by 4.)

In the end, their estimate was 8,500 square feet, approximately double of what David had estimated.  We then critiqued David’s argument and decided that based on the picture only, his calculations were reasonable.  Because we were able to dig for more information, my class believes that their estimate may be a tad more accurate.  Thanks, David for sparking our curiosity this morning.