ideas/thoughts

Watching Solitaire in Silence

Remember Windows Solitaire? I have fond memories playing this fantastic digital distracter with my high school beau on his brand new Gateway computer.  We would take turns striving for success in this card-clicking frenzy, the other watching and waiting patiently for the deck to empty.

But have you ever watched someone play solitaire on the computer?  It is so…what word comes to mind?  Frustrating?  Infuriating?  Aggravating, perhaps?  And why is that?

Check out this screenshot:

solitaire

What if the player was about to click on that blue, flowery deck of cards…would you be fighting the urge to save them from their potentially game-ending error of failing to move the sequence beginning with the six of spades to its rightful place atop the seven of hearts?  Or would you idly sit by and let them to figure out that solitaire is won by carefully searching for card moves before drawing from the deck?  Would you make any suggestions for improving their game once failure was inevitable?

I think this solitaire analogy is a lot like teaching.   I realized fully today why the “productive struggle” is so hard to sustain and perhaps why teachers so often fall back on traditional methods of delivering information to students:  Watching people struggle without intervening is difficult. Just as it’s natural to want to smooth out the path for our children, it’s also tempting to do the same for our students.  It’s just easier (and so much faster) to zip Maria’s (my daughter) coat or buckle her seat belt or pick up her toys.

As a simple, mathematical example, imagine one of your students is attempting to solve a quadratic equation. They start off like this:0126161730-1.jpg

Being the savvy algebra teacher you are, you can anticipate the error that the student is most likely going to make.  You’ve seen it hundreds, if not thousands of times.  Your inner teacher voice might be thinking, “For the love of humanity, Herbie (not your real name), set the dang thing equal to zero!  Quadratic formula!  IT’S GOT A SONG, FOR GOODNESS SAKE!”

Instead, you do not impede their solving and let them continue on their merry, algebraic way. 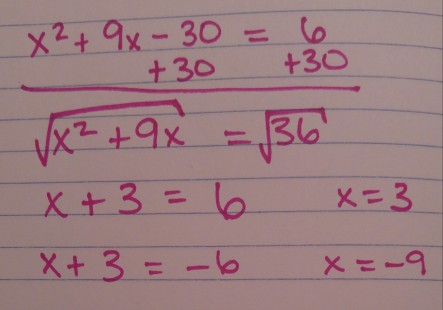 0126161732-2.jpg

Re-enter teacher voice in your head, “Now look what you did, Herbie.  You’ve gone and…wait…one of those answers is right.  Great.  Now we’ve really got issues.”

So what do we do about this?  Clearly the student needs some redirection and the teacher’s role is to guide the learning.  But had we intervened during earlier steps, we rob this student of a golden opportunity for brain growth.  Plus, we deprive the rest of the class the chance to learn from the misconception.  Even more, what a fantastic extension we have here:  why did the student get part of the problem correct and part incorrect?

In summary, we deny students the opportunity to learn from mistakes if we  prevent them from making mistakes in the first place.

Related Side Note:  I’m currently reading The Gift of Failure by Jessica Lahey.  Her introduction about her son’s shoelace-tying trials seems strikingly familiar.  And I can use this antedote as a reminder when encountering the zippers, and the seat belts, in addition to quadratic equations.

 

 

5 CommentsLeave a comment

Safe Spaces at #TMC15

We talk a lot about creating safe spaces for students, but it’s important to acknowledge that teachers need those safe spaces as well.  In many ways Twitter Math Camp IS that safe space where math educators can explore their ideas without judgement and overall be themselves.  But I realized this time around that as inviting as #MTBoS is, it’s ok to seek out further safety nets.

Based on my own experience and what I’m reading on Twitter today, it seems as though there are many of us that need a safety net from the safety.  An example:  everything from Twitter Math Camp ends up on Twitter. There was a presenter who purposefully refrained from using pithy comments simply so they couldn’t be taken out of context on social media.  I’m sure we’ve all experienced a tweet interpreted differently than we intended.

It’s not a secret that I deal with alcoholism.  But this post isn’t about my issue in particular.  It’s about our need, no matter the issue, for a safe space.  And there needs to be safety within the safe places.  Anne Schwartz talks about this in her recent blog post where she talks about surrounding herself with the people she needed after being apprehensive about attending TMC this year.   For Julie, the safe place was the Piano Bar where she could break away and be free to dance with close friends like she loves.

It took me until Saturday to recognize what that safe space looked like for me.  And once I realized it, it was so crystal clear, I can’t believe it took me 2 TMC’s to figure it out.  I don’t mind being around the alcohol one bit, and I don’t want people to feel uncomfortable drinking around me.  In fact, the silliness at the end of the night is usually something I enjoy (sorry not sorry, you guys are hilarious after a few drinks).   BUT at some point in the night, I need a safe place a deep conversation with someone who isn’t drunk.    At TMC14, that person was Justin Aion who walked 1.5 miles with me to get club soda and spent a good deal of Saturday night listening to me.  In Claremont, the sobriety of my pregnant roommate, Teresa, was more important than I realized pre-TMC.  Thank you, Teresa, for just being in the right place at the perfect time.

The patio on Saturday was delightful.  So many people, so much joy, so much community.

But all I could see was the alcohol.  It literally was suffocating me.

I know there were probably lots of you that weren’t drinking.  But the addicted mind sees what it wants, and my imagination had created a courtyard drowning in liquor.  So I returned to my room, texted a friend and called my husband.  This was a powerful realization for me because although those safe places presented themselves organically in previous TMC gatherings, it’s vital that I proactively ensure that safety exists from the get-go.  And that’s what I will do from now on before heading in unprepared.

I know a similar story can be told for a lot of us regarding our interactions in large groups of semi-familiar people.  I would encourage you to look deeply inside and identify the source of your discomfort and examine what can be done to alleviate it.

10 CommentsLeave a comment

Summer Acceptance and Finally Freedom

July 4th. Independence Day. Let freedom ring while we eat a variety of barbecued unmentionables and enjoy pyrotechnicians creating art in the sky.  I hesitated in writing about this because I don’t want my blog to be a venting space, but I realized the eclectic nature of my posts are what make it uniquely mine.

Backstory:  Getting through the spring trimester seemed insurmountable because on March 2nd, a gentlemen, presumably heading to work just as I was, failed to look in the direction he was driving and smashed into my car.  My car was totaled and the base of my thumb was crushed by the airbag.

What was hurting me most though, was the resentment I had over this injury and the recovery over which I had no control.  And when you are an alcoholic, resentment has the power to destroy, and I felt very powerless over letting it tear me apart.  I barely got myself out of bed on weekends and paid little attention to my daughter and husband.  I ignored emails from my mom and shut myself out from letting her help me. I lashed out at people on Twitter, both overtly and in subtle ways.  I pushed away friends and neglected relationships, some of which I may not be able to recover.

Step Ten of Alcoholics Anonymous states, “Continued to take personal inventory and when we were wrong, promptly admitted it.” I’m thankful that I am a teacher for a multitude of reasons, and the summer off is giving me the time to find clarity and strength to rebuild what I have broken down in my state of depression.  Since school has ended, I have gotten myself out to visit with the three dimensional people on weekends, and I’m working on interacting more positively on Twitter.  I’m trying to repair broken relationships with people I pushed out of my life especially my mom, who I know always loves me.  And I’ve spent quality time with my child and my spouse.  And I am happy again. Genuinely joyful and self-accepting.  And free form the burden of resentment.

I went to an AA meeting recently, and someone made a reference to a paragraph in the Big Book on acceptance.  I marked it, have read it many times in the last few months, and am going to end this post with it:

And acceptance is the answer to all my problems today.  When I am disturbed, it is because I find some person, place, thing or situation unacceptable to me, and I can find no serenity until I accept that person, place, thing or situation as being exactly the way it is supposed to be at this moment.  Until I could accept my alcoholism, I could not stay sober; unless I accept life completely on life’s terms, I cannot be happy.  I need to concentrate not so much on what needs to be changed in the world as on what needs to be changed in me and in my attitudes.

Alcoholics Anonymous Big Book, Chapter 16, page 417

12 CommentsLeave a comment

The Stupidity of Number Flexibility (#TMWYK)

I’d compare the struggle between teachers and learners at the end of the year to that of a parent trying to carry a limp child to their bed.  Eventually they will both get there, but the parent is frustrated and the child is attempting to make things as difficult as possible.   In the end, neither party is probably happy.

Rather than focus on that inevitable struggle, I want to detail a fun experience (for me) that I had with my daughter this past weekend. Her four-year-old rebellion has included a resistance to completing her math and language at school and a refusal to engage in those conversations at home.  Grandma and Grandpa were in town this weekend, which gave me an opportunity to exploit her desire to impress them.

At school, Maria is given “problems” similar to the ones on this sheet.  They seem randomly chosen, and the children are given beads to model the problem if needed.  0526150926-1

 

Given the opportunity to exploit the situation, I handed her 12 beads and wrote down 4 + 4, 5+3. 3+5, 2+6, 6+2, 1 + 7, and 7+1.

After protesting that 5 + 5 (her favorite after 4 + 4) wasn’t on there, she started sorting the beads into two piles.

countingbeads

I noticed:

  • She knew 4 + 4 by memory and did not use the beads. (Same with 5 + 5)
  • She sorted 5 + 3 into a pile of 5 beads and a pile of three beads.
  • She did not grab the beads to do 3 + 5 but rather recognized it was the same two numbers and therefore totaled 8.
  • 6 + 2 required her to count the beads but she did not grab new beads.  She simply rearranged the original piles.
  • At 2 + 6 she was onto me and simply filled in “8” for the remaining answers.

Maria:  Mommy, this math is stupid.

Me:  Why do you think it is stupid, my sweet little bucket of sunshine?

Maria:  All of these are the same answer.

Me:  And what makes that stupid to you?

Maria:  It is just stupid.  Math is stupid. I never want to do math again.

(Awesome.)

This reaction makes me very curious about where her feelings of “this is stupid” comes from.  She’s only 4.  She has much less experience with “answer getting” than, say, a teenager.  Yet, her evaluation of the task being “stupid” seems to stem from the idea that if the answer is always the same, why do the problem in the first place?  Is the mentality of “answer over process” more innate than we think?  Or is it simply so pervasive in our education system that even my 4 year old has picked up on it?

Number flexibility is something I’ve made routine in my classroom as of late.  Detailing different strategies to arriving at the same result gives students a stronger foundation on which to build algebraic thinking.

Sigh.  It might be a long summer, but she’ll learn I don’t give up so easily.

0 CommentsLeave a comment

Dear Students: No. I’m Not Sorry.

Picture from: http://www.advantagecapitalfunds.com/blog/wp-content/uploads/2013/10/I-Promise.jpg

I read a very moving blog post in which a teacher apologizes to her students for the problems plaguing our education system and hold students back.  While I agree with Lizanne Foster’s view on the way schools are structured, I felt she was taking blame for elements of students’ experiences over which she has no control.  I wanted to follow her blog up with a reminder that students don’t need teachers to feel sorry for them; they need teachers to empower, inspire, and motivate them to do better when they leave the classroom than they did when they entered.

Although you have to be at school so early each morning, I promise to make those early morning minutes worth getting out of bed for.

Even though you have to ask permission to use the restroom, I promise to respect your good judgement for appropriate times to leave the classroom.

I promise to create opportunities for you to get out of your seat and move about.

I promise that even though you are pre-grouped by age, I will provide you with problems that engage all levels of intellect:  problems that stretch you as well as provide scaffolding as needed.

I promise to create an environment where you feel safe in making mistakes.

I promise to allow you to solve problems collaboratively because I know “together” is where the best solutions come from.

I promise to work hard to provide the support you need to further your learning.

I promise to do my best to help open your mind to subjects and ideas that may have once seemed boring.

I promise that you will have my respect at all times and do not have to earn it.

I promise to never make you compete for grades.

I promise to give you opportunities to apply mathematics to solving our world’s economic, environmental, and political problems.

I promise to encourage curiosity throughout your learning experiences.

I promise to always let you examine, explore, experiment and experience.

I will try every day to re-ignite your passion for learning you had when you were young.

I will attempt to bring out your inner-scientist/writer/architect/artist whenever I am able.

I accept and understand that you were born to learn and that memorizing is not learning.

I promise to never make you feel that the only learning that matters is learning happening in a classroom and I promise to never focus your learning on just what will be covered on the test.

I promise to facilitate as much “out of the box” thinking as I can and will always present problems that allow for multiple solution paths.

I am mostly powerless over these powers-that-be that determine funding for your education, but I will do anything I can within my control to make learning in my classroom a positive experience for you and your classmates.

Sincerely,

Your Teacher

 

2 CommentsLeave a comment

Matchmaker, Matchmaker: The Algebra Way

I’m trying to make my blog less OMG-you’ve-got-to-try-this-amazing-activity-that-I-found-cuz-it’s-awesome and more analysis of my teaching and an examination of where improvements can be made. That being said, this post is going to be a little of both.

Today, my Algebra students did another Talking Points activity on linear functions.  I used the same format I did with Number and Operations where I gave them 5 minutes to look over the TP’s and make any notes they needed for the group activity.  Here’s the link if you are interested in seeing what they chatted about.  As I honed in on their exploratory talk, I noticed that many more of them were convinced by the reasoning of their tablemates and changed their “unsure” to “agree/disagree.”  I’m not sure if that was because the topic was a tad more difficult, or if they are getting better at listening to one another.  Of course, I am hoping it’s the latter.

At the end, after they wrote their self-assessments, we talked as a group about some of the points that they were still not convinced of agreement or disagreement (which included The opposite reciprocal of zero is zero).  I tried to do this using the Talking Points rules, even though the whole class was able to participate in the discussion.  I feel that this was a positive addition to the process.

 

Okay, onto the real star of today:  An Nrich Task. 

Each group of 4 receives a pack of 16 cards with algebraic expressions on them.

algebra match image (1)

They cannot take cards from other group members; they may only give cards to others.  Each person must have a minimum of two cards in front of them at all times, to alleviate the temptation of having one person sort the cards.  To complete the task, each group member must have four cards in front of them that have the same simplified expression.  Caveats:  no talking, no non-verbal communication, no writing, no taking others cards.

I used the Glenn Waddell #TMC14 Smartphone Camera Hack to position my camera in the back of the room and I took a time-lapse video with my old iPhone.  Although I can’t post that video online because it contains images of students, I did make a screenshot with blurred faces:

7ffc57b177e951e8030a53db5e873e1b

I mean, you can practically SEE the brain sweat pouring from their ears!

In our debriefing, we discussed what was hard, what was easy, and what strategies they developed.  Here are some highlights:

  • It was nice to be dealt a card that was already simplified.
  • Besides not being able to talk or non-verbally communicate, it was difficult to simplify some of the expressions mentally.
  • It was difficult to not take cards from others, knowing where they belonged.
  • A good strategy when starting was to see if there were any matches to begin with.
  • Another good strategy:  give unsorted cards to players who have completed sets so that they can help divvy those out.

I was so impressed with these kids today.  I know that they will learn more together by working with one another.  I’m so thrilled that THEY are beginning to see the truth to that.

 

0 CommentsLeave a comment

Making a Point

Our school uses a 5-period, trimester schedule which means that every 13 weeks, I have a new group of angels in my classroom.  I decided to give Talking Points another try, with the goal of incorporating some exploratory talk related to the topics in our units of study.  Additionally, the practice of “no comment” has proven to be undeniably helpful in encouraging students to listen to one another.  [Note:  Elizabeth Statmore introduced these at Twitter Math Camp this summer.  See the “Talking Points” link for more information.]

My goal is the same:  Addressing status in my math classroom and allowing every kid to have a voice. I began with the math talking points and then transitioned into some talking points related to our current unit: Numbers and Operations.  (I’d love to have the students come up with their own talking points as well, although I haven’t tried that yet.)

In their self-assessment, I asked them how difficult it was to practice “no comment” and was quite pleased with some of their responses.  In particular, the student that explicitly stated that he failed in refraining from commenting.  It was an excellent opportunity to encourage them to be better the second time around.

Something awesome that I noticed today:  students respectfully called each other out on cross-talking violations.

Here are the talking points we used today:

Talking Points – Number and Operations

  • The sum of two fractions always results in another fraction.
  • There are an infinite number of fractions between any two fractions.
  • Using a fraction is always a more precise answer than using a decimal.
  • The commutative law of addition (a + b) + c = a + (b + c) only works for positive numbers.
  • For the fraction -x/y, it does not matter if x is negative or y is negative as long as one of them is.
  • The reciprocal of a number is usually smaller than the original number.
  • The square root of a number is always less than or equal to the original number.
  • Zero is neither even nor odd.
  • Taking a positive whole number to a power always results in a larger number.

When having them assess themselves the second time around, many commented that it was much more difficult not to comment immediately.  Although some of the points are intentionally ambiguous, a number of them have right and wrong answers.  Conversely, the topics yesterday were more general “math opinion” related bullets.  Fortunately, when listening to their conversations, I found that many who struggled yesterday improved on today’s task.

I’m encouraged by my take on this activity this trimester.  I think that centering the statements around our units will be helpful in examining mathematical statements that make students think critically and support their decisions.

 

0 CommentsLeave a comment

Female Feelings and Brash Boys??

It’s Friday, it’s Halloween, and our football team is playing tonight in the section finals for the first time in about 30 years.  To think that solidifying understanding of domain, range, increasing and decreasing functions was going to be a priority for my college algebra class was a farce and so I decided to make the class more productive.  We watched the Simpsons. And I ate my weight in Swedish Fish.

Image from Wikipedia

Image from Wikipedia

Girls Just Wanna Have Sums pokes fun at the stereotype that men do better in math and are inherently aggressive and women want to sit and talk about their feelings.  Consequently, Springfield Elementary is divided into a girls school and a boys school which embody those stereotypes.

http://player.foxfdm.com/simpsons/embed-iframe.html?videourl=http://link.theplatform.com/s/fng-fx/tO87mhBBqh5L?mbr=true&policy=

(If you weren’t aware, every Simpson’s episode ever created is available on FX’s new website, Simpsons World.)

After the show, I asked the students to write about their feelings on this stereotype and how it plays out in the United States.  I then asked them to describe a satirical jab that they found particularly disturbing or upsetting.  As a math teacher, I sometimes lack the inclination to ask students how they feel on a particular controversial topic; but I’m always glad when I do ask.  Acknowledging differences that exist in the ways males and females approach math is important.  But this episode was more about educational access to high level mathematics.

The majority of what they found disturbing was that the girls weren’t given the same opportunities as the boys to experience challenging mathematics.  As I responded to their submissions, I took the opportunity to push their thinking further and ask “Are there instances, other than gender, where students are not given the same educational opportunities?”  I hope that my feedback will foster a dialog about the importance of all students having access to a high quality education, beyond inequalities based on gender.  Because these inequalities exist, maybe not based on gender, but definitely based on race and socioeconomic background.  I’d like to continue to help them think about what that means for those students.

0 CommentsLeave a comment

What Questions Do They Have?

I’m always delighted by the extra wave of energy students put forth when they are asked to develop their own question to a scenario.  I love my job, and this year has started amazingly.  But today was probably my favorite day thus far.

College Algebra:  

Since we are working on quadratics, we did the Many or Money scenario from the Math Forum Problems of the Week.  It’s interesting (and almost entertaining) to watch them discover that there is no question.  This is the first time we’ve done an activity where they developed the question so they came up with the questions I would have expected:

  • What price will maximize profit?
  • How many students would go if the price were $8?
  • How many students will attend at the maximum profit?
  • (My favorite) Can you write an equation that models Ticket price and Profit?

They were able to get started on answering some of these questions.  I had them work on one large sheet of paper in order to share their work.  The period ended before they could wrap up their work.  Here is what one group has so far:

1008141405-1

When talking with teachers about using the Notice and Wonder strategy is usually surrounding the unexpected “wonderings” that students will have.  I think it’s important to allow them to have that creativity of asking outlandish questions like, what is the band’s favorite pre-concert meal?  But to make sure that the math goals are met, shifting their focus on what we can mathematically deduce from the scenario.  I usually ask what would I most likely ask about this scenario and what questions do you have about this scenario?  

 

Algebra 2:

Last year, with this same class, we examined Val’s Values.  The authentic, real-world awesomeness of that particular lesson was going to be impossible to re-create, but the scenario was still applicable and intriguing to this new group of students.

Last year, my students insisted that the ages of both Val and Amir were vital to answering the question Who spends more on jackets over their lifetime?  Most fascinating to me was their estimations of Val and Amir’s ages:

1008140948a

Desmos made up  a nice scatter plot for us that we could also Notice and Wonder about:

7dzmdvzq1g

And Val, my students were slightly disappointed that they didn’t get to examine the entire $300 jacket.  They are VERY curious about it.  😉

 

 

0 CommentsLeave a comment

If You Give Homework, I’m Talking to You

Maybe it’s because it’s Friday and this has been one action packed week, but I am FIRED UP.  I’m fired up about the amount of out-of-school homework we give our students, especially in math class.

Casey Rutheford had a great idea the other night.  He did a Twitter search for “math homework” and examined the results.  Go ahead and take a look for yourself.  You may not be shocked at all, but reading tweet after tweet of math homework making students cry should make you, as an educator, want to sob.   Additionally, with impeccably good timing, John Stevens gave us all something to think about in regards to the homework debate.  The entire post is worth every second of time you can spend with it.  He highlights the student voices in this conversation.  Those voices are the ones we often aren’t really listening to.  He reminds us that there is a whole child to develop, not just a math brain.

The big question I have for my fellow educators is:  are you taking the time to listen to your students’ voices?   Are you considering the education of the whole child, especially during the hours when they aren’t in school?  What purpose does the homework serve?  Is it really fulfilling that purpose?  Do we really feel students do better as a result of homework, or are there other factors that play a much bigger role?

I’m not saying don’t ever assign homework.  I just don’t think homework needs to be a knee-jerk reaction to the end of a math lesson.

 

 

 

 

 

 

2 CommentsLeave a comment