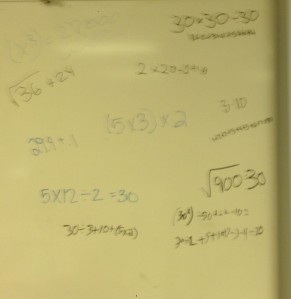Month: May 2014

Yesterday:  As much as I get frustrated by the attitudes and actions of my 5th hour, much of my resentment stems from the fact that I believe the situation in my class is my fault.  I feel like I’ve conditioned them by accepting disrespectful behavior in order to keep kids in the classroom.  As a result, the entire learning environment has suffered.

Today: So that was the beginning of yesterday’s post. I was concerned going into today’s class. Last Friday of the year and the fact that the school has been a circus compounds the issue. I was expecting chaos, but what I got was mathematical success. The difference was I demanded their attention in a more respectful way. I was firm, but polite, and it payed it’s dividends in student engagement.
We began with a simple math talk that I modeled from Fawn Nguyen’s March 21st math talk:

Today is the 30th day of the month.  Write as many equations you can that equal 30.

I gave them about 5 silent minutes. Then I let them use their calculators to come up with more gems.  At the end, I had them share their favorite or most complicated equation on the whiteboard.

IMG_5388 IMG_5389 IMG_5390

 

Here’s where the real magic happened.

Me:  Look up here and see if there are any equations you disagree with

Lots of discussions ensued about order of operations, square roots, rounding, parentheses, etc.  Overall, the activity lasted 30 minutes, which was about 29 more minutes of math than we did yesterday.

But the fun doesn’t stop there.  To boot, I introduced the Mathalicious Decoder Ring Lesson.  We watched the Christmas Story clip and talked about what a decoder ring does.  What I liked is that most of them were trying to figure out how the decoding worked, rather than just “get the worksheet done.”

Justin Aion stated poetically on his blog today the exact way I feel about this class:

We teach students long-term strategies to accomplish short-term goals and often don’t see any progress.  If we are very lucky, we’ll see the kind of growth we want by the end of the school year, but the growing season on students isn’t as regular as it is for other crops.  Each seed needs its own time to grow.We desperately need to get away from the notion that if it hasn’t sprouted by the beginning of June, then it must be a defective seed.

1 CommentLeave a comment

Brain Sweat

I’ve talked about my Algebra 2 class at length on this blog over the last 2 months, and as the trimester comes to a close, I want to celebrate the positives in this class as much as possible.  They frustrate me sometimes, but the bottom line is I’m willing to fight and fight hard to make their experience with math more positive.  Ultimately, they’ve been dealt an unfair hand:  crammed into giant classes and labeled incapable of high-level mathematics.  They are capable of more than they give, but they also deserve much more than they’ve been given.

The perpetual optimist in me wants to continue to celebrate their achievements and play the hand they’ve been dealt as best we can.  Today we took on Robert Kaplinsky’s Cheeseburger Lesson.  I’m not sure why I’m constantly drawn to this lesson, since the picture of the 100×100 makes me a little ill.  Perhaps it’s the constant student engagement I get from it, time after time.  The intriguing thought that someone actually purchased this godzilla-burger hooks students every time.

What I liked most about my class’s efforts toward this task was the multiple revisions they had before arriving at the correct answer.  I had many students assume that a 3×3 cost the same as three cheeseburgers, only to find that their burger only needed one bun.

Below is a student’s work that I really appreciated.  At the end of the activity, he said,

“Mrs. Schmidt, I’m sweating.  I thought so hard on this problem that I’m sweating.  But I believe I have the right answer.”

photo 5

If I’m being completely honest overall, this class has tested me, day in and day out.  I’ve worked very hard, but in the end, I’m not sure I taught them much of anything worthwhile.  I hope I have, but I’m not sure I did.  A class size of 36 seemed insurmountable, and perhaps in some ways, I never really overcame it.  Unfortunately, next year’s class size projections promise more of the same.  The silver lining, however, is that I get another crack at teaching this same course, and I’m 100% sure I can do it better the next time around.

1 CommentLeave a comment

Probability Ponderings

It’s been a great week in my probability and statistics classes.  I’m not sure why I’m pleasantly surprised.  This time of year it’s absolutely essential that we engage kids in meaningful mathematics and when we do, they respond well.

Monday, we did expected value and Dan Meyer’s Money Duck.  See Monday’s blog post for details.  Extra Credit if you can find my duck pun in there.

Tuesday, after assessing expected value, we moved to tree diagrams and conditional probability.

Wednesday, I used Nrich’s In a Box problem to create some discussion about dependent and independent events.  

I started with a bag with unifix cubes and had them do some experimenting to see if the game was fair.  What I love about this problem is that the initial answers that the kids come up with are usually completely wrong.  It really allows the teacher to identify the misconceptions.  Additionally, this problem is so easy to extend.  Simply have the students come up with a scenario of ribbons that creates a fair game.  Most will come up with something like 2 red and 2 blue. Have them test their theory, find out it’s wrong and then test another.  Even when they find the magic combination that creates a fair game, there is still the task of generalizing the results that’s challenging.     

Thursday, I totally stole Andrew Stadel’s 4! lesson.  What a great intro to the idea of factorial.  Last trimester I used IMP’s ice cream bowls and cones, which I still might refer to.  I felt like having a few students up in front at the beginning got everyone on the same page at the same time.  It was completely awesome to see the different methods for solving this.  I love the repeated reasoning here:

photo

Plus, opportunities to use animal counters in HS math are scarce.

What’s the most pleasing about this week is that I think that this group’s conceptual foundation of these concepts is more solid than it has been in any previous year.  We still have practice to do, but I feel like they have made a good connection to what their answers represent.  In the past, my formula driven instruction didn’t bode well for retention of the concepts. I’m more hopeful this time around.

1 CommentLeave a comment

Thanks Ashli for the spectacular idea of sharing what adorns our classroom walls.  I’ve got the regular math posters, sports schedules, school policies, and motivational cliche’s, of course.  A classroom would not be complete without a stock photo along with transformational words like, “the key to success is self discipline.”

What really brings me the most joy in my classroom and truly makes my classroom mine is my dog wall.

IMG_5286IMG_5287

Ok, it’s actually two walls.  Backstory:  I love dogs, beagles in particular.  Duh.  But the reasoning behind my dog wall runs deeper than that.  Yep, the dogs are adorable and the kids love that they can put a picture of their own dog in my room.  I love it when I have younger siblings of former students, and they ask “hey, you have a picture of my dog!”

The real power behind the dog wall is acknowledging what dogs can teach us about love.   In short, no one on earth is capable of loving you as much as your dog.   Oprah gives us a nice example when remembering her cocker spaniel, Sophie.  If you have a dog, you know what I’m talking about.

I recognize that not all students are lucky enough to own a dog.  I also let them bring in a picture of any dog, but I make sure to mention that I like beagles best.

My plans for the expanding dog wall include using them for some estimation and data exploration.  Someday.

4 CommentsLeave a comment

Authentic, Value-Added Algebra

About a month ago, my algebra class was working on the Math Forum’s Free Scenario called Val’s Values.  

There was a lot to question here (which they did) and a lot to wonder (which they did as well).  Something that was unsettling, however, was that they did not know the age of Val or Amir which they felt was pertinent to answering a major question:  Who has spent more on jackets in his/her lifetime?

We made some age estimates and answered our own question as best we could, but it felt less authentic than it could have been.  So, we submitted a comment on Valerie’s blog and today our attention to precision was answered with a response.

I gave my class another go at figuring out who spent more on jackets.  Here are a couple of their responses:

IMG_5293 IMG_5291

What impressed me overall with their approach to this problem was not necessarily the mathematics itself.  The magic was in their careful identification of important variables and analysis of what mattered and what didn’t.  Additionally, they were able to look past the “right” answer and truly own THEIR answer from THEIR assumptions.  I had very few students ask Is this right?  Instead, they were communicating their methods with one another and challenging the reasonableness of their results.  The spark:  the flexibility of the scenario and the real response from a Math Forum Team Member willing to help add some authenticity to a classroom task.  Thank you, Valerie Klein.  We appreciate it.

 

2 CommentsLeave a comment

Duck, Duck, Money Duck

When I moved to Minnesota, I learned a new game called Duck, Duck, Gray Duck.  This is similar to the game that the rest of the country cleverly calls “Duck, Duck, Goose.”  Evidently, in Minnesota, as you are tapping heads, you can call out absurdities such as purple duck or yellow duck.  Listening skills at work here; gray duck is the magic color.

[The preceding paragraph has nothing to do with this post, but if you’ve always wondered why Minnesota boasts Duck, Duck, Gray Duck rather than conforming to the rest of the country, now you know.]

Speaking of ducks, Dan Meyer’s newest three-act lesson was coincidentally timely with my probability and statistics progression.  Today’s learning target included expected value, so I thought we’d give it a go.

Act 1, Initial Questions:

  • Can you actually buy one of those?
  • Is that like the diamond ring candles?
  • Do any of them have $50, for real?
  • Would it be worth it to buy a bunch to get the $50?
  • How much do those things cost?

I had them speculate a fair price for one of these duck soaps.  We had a discussion about what was meant by “fair” which was productive.  Most students settled on a price between $3 and $20.  The students also wanted to consider if shipping was included in our pricing.  Since we were looking at the price from the Seller’s point of view, it made us wonder if the shipping for Amazon Prime products is passed along to the seller or absorbed by Amazon.  We’ll have to address that another day.

Notables in Act 2:

1.  When deciding which probability distributions were impossible, students were quick to point fingers at E and F.

moneyduck2.002

 

After making the connection that the total of all bars must equal one, most students were able to identify B and C as impossible.  Arguments ensued over D about whether the two bars would total 1.  The ruler confirmed that indeed the bars did not add up to 1.

2.  When looking at these distributions and determining how a $5 duck would be bad for business, my students noticed something interesting.

IMG_5283IMG_5284IMG_5285

We had some great conversation about which would be worse:  losing customers from a faulty product or losing money with too many rich ducks.

3.  When determining fair prices for these distributions, I was impressed with my class’s use of an area model.  I sometimes supplement the probability unit with activities from IMP’s The Game of Pig and liked their application of a ruggish diagram here.  This allowed for a more fluid connection between the value of the duck bill and the probability of that payout.

moneyduck2.004IMG_5282

 

These are 9th graders, so only a few requested the sequel.    Overall, I was pleased with the outcome of this lesson.  I feel like the the money duck grabbed their attention more than previous attempts at real-world expected values such as pull-tabs or roulette.  I think the kids felt like soapy money is something they can access, and I think their attention to the task reflected that.

 

 

7 CommentsLeave a comment

Buried Bias

Another provocative post coming at you.  You’ve been warned.

Probability and Statistics classes always rejoice on the days that I teach them how to play dice games.  Today it was Pirate’s Dice (or Liar’s Dice).  I love using this game because it’s simple to learn, fun to play, and actually requires the use of probability rather than just luck.  I found this article in NCTM from December 2012 and have modeled my activity after theirs.  That article is behind a paywall, so this link will tell you how to play the game if you are interested.

Overall, the student’s enjoyed the game and most of them got into it.  I had to move a few groups away from the shared wall because they got a little too excited, but overall, I felt like my goal for them was reached.  Most of them used probability to create a strategy to help them win.  I had lots of students tell me that the game was fun, so you’d think I would just close the week and move on.

Here was the problem:  in one of my classes, I had a group of students who barely participated.  They were in groups of their choosing, alleviating the idea that they can’t work together.  They positioned themselves in the back corner and once I was off helping another group, all members promptly dug their faces into their phones, texting, tweeting, and snapchatting away as if they were sitting in the cafeteria rather than math class.

I definitely could have handled the situation better because I got MAD at these kids.  Not yelling (because I don’t yell ever), but angry, defensive, and accusatory.  They got back to work.  Sort of.

I stepped back from what just happened to assess why their actions set me off in such a way.  A few other kids were on and off their phones when it wasn’t their turn to bid, and I wasn’t angry at them.  Was it perhaps because it was an entire group of 6 people that were disengaged?  An easier target?

I’ve had enough psychotherapy to know that  this had little to do with the fact that those kids weren’t playing as directed.  This had to do with the fact that this group of kids were the “cool kids.”  These were the popular, tons-of-friends, high-status 9th graders who always have a place to sit at lunch, who have a locker in the center of the hallway, and who would have never given a kid like me the time of day in high school.

Nailed it.  My frustration and resentment toward this group of kids had more to do with how I was treated by their “type” when I was in high school than their inappropriate behavior at that moment. In fact, had I nicely told them to get back to work, who knows, they might have happily complied.  Maybe not, but that’s not the point.  The point is that I didn’t give them that opportunity because my reaction was out of emotions from my high school experience.

I don’t do this often, and I’m glad I recognized it right away.  Right or wrong, these kids deserve a teacher that fairly and consistently applies her classroom management philosophies.  And students shouldn’t have to bear the brunt of their teacher’s lasting scars from a high school experience. I’m glad I’m aware enough to recognize this and change my actions.

1 CommentLeave a comment

Etcetera, etc….

I love it when students figure stuff out.

I love it even more when:

A.  Students figure out things that, as a teacher, I didn’t  notice myself.

B.  Students who are labeled as “not good at figuring stuff out” figure stuff out.

Here’s what we did today in Algebra 2:

number pyramids

This is a SMILE resource from the National STEM Centre.  The problem I thought I would encounter is the word “etc.”  Kids don’t do well with “etc.” Etcetera is vague, non-committal, and easily dismissed.  To a student, etcetera usually means “I’ll ignore this and see if no one notices.”

It is helpful for me to be more specific with my expectations of students, especially when their mathematical well being is at stake.  But today, I was feeling a little vague and non-committal myself, so I handed out the sheet, explained what was going on and let them go…etc.

There are no words I love to hear more in my classroom than “Mrs. Schmidt, look what I figured out.”  And today was chock FULL of those statements.  Here are a few:

  • The triangles are always as wide as they are tall.
  • The sum of the base of triangles 3-wide is 3/4 of the top number.
  • As the triangles get larger, the percentage of the peak number gets smaller.
  • The percentage decrease is related to the size of the triangle
  • If the triangle has an odd numbered base, then the center number in the base is always related to the peak number.

There were lots more.  I was very proud of this class’s resolve in addressing the Etcetera.

 

1 CommentLeave a comment

Dice Wars

Nrich has an interesting activity called “Non-transitive Dice” that I’ve always wanted to use in my probability and statistics class.  I’m intrigued by the relationship between the strategy in choosing a dice and the probability of winning with that dice.

We don’t have blank dice, so I had my students make their own with cardstock.

IMG_5239

 

Initially, I had them choose which dice would win overall.  Then we let the rolling begin:  A vs. B, B vs. C, and C vs. A.  As they collected their data, they started predicting which dice would end up on top after battle.

Tomorrow, I’d like to sum up the probability representations of some of the dice match-ups.  I found this nice post by James Grime (yep, the Numberphile chap) with a few varieties of non-transitive dice.  Next year, I might start with his Grime set and have students collect data on different matchups.

If we are successful, hopefully we can workout the probability of these outcomes.

http://grime.s3-website-eu-west-1.amazonaws.com/

And finally, I know that my students will want to compare this dice game to Rock – Paper – Scissors – Lizard – Spock.

File:Rock Paper Scissors Lizard Spock en.svg

http://upload.wikimedia.org/wikipedia/commons/f/fe/Rock_Paper_Scissors_Lizard_Spock_en.svg

I kept digging into James Grime’s rabbit hole and realized, you can purchase this set of non-transitive dice.  Skippy.  I might do that!

0 CommentsLeave a comment

#TMWYK – The Return of the Sand Pool

It’s a tough time of year for teachers, and I don’t say that to garner any sympathy.  But I’m going to take a moment to deviate from the regular musings of my classroom and write about my favorite topic:  my daughter.  The discussion won’t be completely unrelated as I have learned a great deal about my students’ development of mathematical literacy while watching my daughter make sense of numbers, quantities and shape.  And of course, Christopher Danielson’s development and facilitation of Talking Math with Your Kids has encouraged me to continue the conversation with my own child.  Specifically, I appreciate that his daughter is a few years older that Maria so that I know what I’m looking for and what to look forward to.

Maria (3.5 years old) loves to be outside.  As soon as the snow melted, she insisted that it was now summer and hence every activity from that moment forward must be done in the great outdoors.  A personal favorite is the sandbox, with water.  I’m not opposed to the sandbox overall, but mixed with water, it becomes more like a swamp.  Plus, let’s face it.  It’s Minnesota. It’s Spring, not Summer, and taking out the hose just isn’t in the cards just yet.

So we made a deal that when the temperature on my weather app reached 70 or above, we could take out the hose.  In the mind of my three year-old, this meant that the first of the two digits needed to be a seven.  On Saturday, this lucky girl got to take out the hose.

IMG_5229

Results as expected.

IMG_5230

 

Sunday, I decided to test Maria’s understanding of these numbers.  She again asked “is it seven on the phone?”  I instead showed her Chicago’s temperature which was a balmy 82 degrees.    As expected, her response was “Aww, it’s not seven so we can’t do water.”   I know she knows 8 is bigger than 7, but hasn’t yet connected that a temperature that begins with an 8 represents something warmer than a temperature that begins with a 7.

 

 

0 CommentsLeave a comment