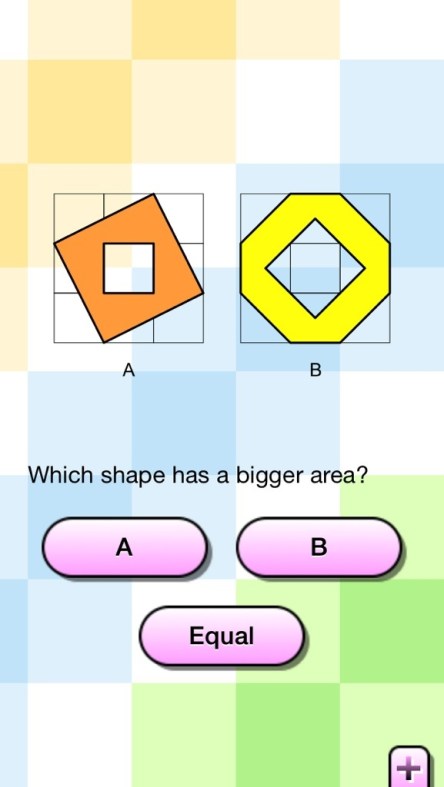
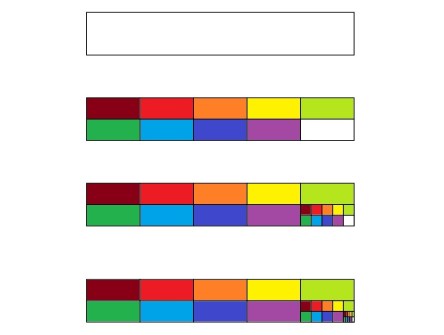
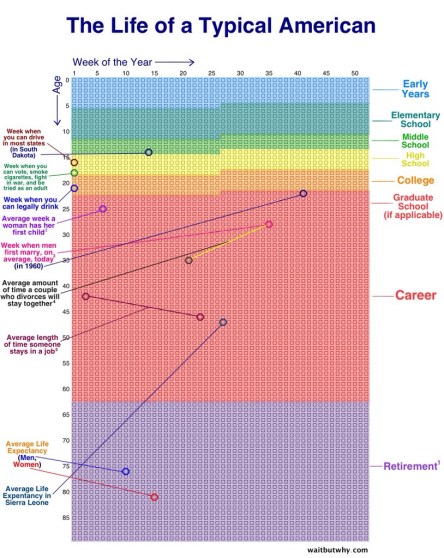
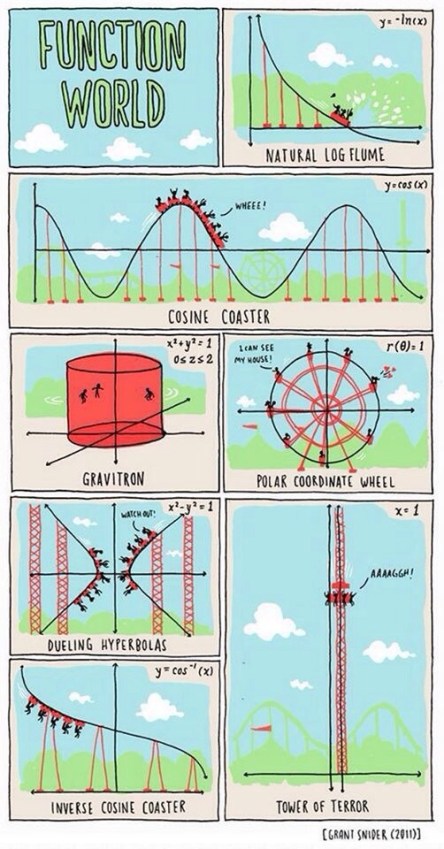
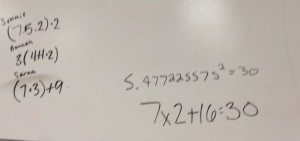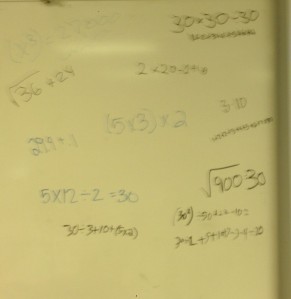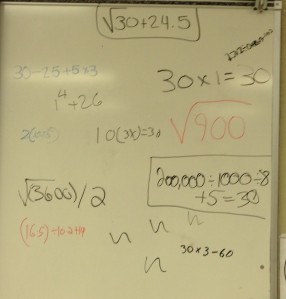Scrolling through my iOS Camera Roll, I realized that I have saved quite a few graphs, problems, charts, inforgraphics, and miscellaneous mathematical quirkiness. I have yet to really do anything with these but I’m going to share them here to hopefully inspire myself this summer.
Yesterday: As much as I get frustrated by the attitudes and actions of my 5th hour, much of my resentment stems from the fact that I believe the situation in my class is my fault. I feel like I’ve conditioned them by accepting disrespectful behavior in order to keep kids in the classroom. As a result, the entire learning environment has suffered.
Today: So that was the beginning of yesterday’s post. I was concerned going into today’s class. Last Friday of the year and the fact that the school has been a circus compounds the issue. I was expecting chaos, but what I got was mathematical success. The difference was I demanded their attention in a more respectful way. I was firm, but polite, and it payed it’s dividends in student engagement.
We began with a simple math talk that I modeled from Fawn Nguyen’s March 21st math talk:
Today is the 30th day of the month. Write as many equations you can that equal 30.
I gave them about 5 silent minutes. Then I let them use their calculators to come up with more gems. At the end, I had them share their favorite or most complicated equation on the whiteboard.
Here’s where the real magic happened.
Me: Look up here and see if there are any equations you disagree with
Lots of discussions ensued about order of operations, square roots, rounding, parentheses, etc. Overall, the activity lasted 30 minutes, which was about 29 more minutes of math than we did yesterday.
But the fun doesn’t stop there. To boot, I introduced the Mathalicious Decoder Ring Lesson. We watched the Christmas Story clip and talked about what a decoder ring does. What I liked is that most of them were trying to figure out how the decoding worked, rather than just “get the worksheet done.”
Justin Aion stated poetically on his blog today the exact way I feel about this class:
We teach students long-term strategies to accomplish short-term goals and often don’t see any progress. If we are very lucky, we’ll see the kind of growth we want by the end of the school year, but the growing season on students isn’t as regular as it is for other crops. Each seed needs its own time to grow.We desperately need to get away from the notion that if it hasn’t sprouted by the beginning of June, then it must be a defective seed.
Another provocative post coming at you. You’ve been warned.
Probability and Statistics classes always rejoice on the days that I teach them how to play dice games. Today it was Pirate’s Dice (or Liar’s Dice). I love using this game because it’s simple to learn, fun to play, and actually requires the use of probability rather than just luck. I found this article in NCTM from December 2012 and have modeled my activity after theirs. That article is behind a paywall, so this link will tell you how to play the game if you are interested.
Overall, the student’s enjoyed the game and most of them got into it. I had to move a few groups away from the shared wall because they got a little too excited, but overall, I felt like my goal for them was reached. Most of them used probability to create a strategy to help them win. I had lots of students tell me that the game was fun, so you’d think I would just close the week and move on.
Here was the problem: in one of my classes, I had a group of students who barely participated. They were in groups of their choosing, alleviating the idea that they can’t work together. They positioned themselves in the back corner and once I was off helping another group, all members promptly dug their faces into their phones, texting, tweeting, and snapchatting away as if they were sitting in the cafeteria rather than math class.
I definitely could have handled the situation better because I got MAD at these kids. Not yelling (because I don’t yell ever), but angry, defensive, and accusatory. They got back to work. Sort of.
I stepped back from what just happened to assess why their actions set me off in such a way. A few other kids were on and off their phones when it wasn’t their turn to bid, and I wasn’t angry at them. Was it perhaps because it was an entire group of 6 people that were disengaged? An easier target?
I’ve had enough psychotherapy to know that this had little to do with the fact that those kids weren’t playing as directed. This had to do with the fact that this group of kids were the “cool kids.” These were the popular, tons-of-friends, high-status 9th graders who always have a place to sit at lunch, who have a locker in the center of the hallway, and who would have never given a kid like me the time of day in high school.
Nailed it. My frustration and resentment toward this group of kids had more to do with how I was treated by their “type” when I was in high school than their inappropriate behavior at that moment. In fact, had I nicely told them to get back to work, who knows, they might have happily complied. Maybe not, but that’s not the point. The point is that I didn’t give them that opportunity because my reaction was out of emotions from my high school experience.
I don’t do this often, and I’m glad I recognized it right away. Right or wrong, these kids deserve a teacher that fairly and consistently applies her classroom management philosophies. And students shouldn’t have to bear the brunt of their teacher’s lasting scars from a high school experience. I’m glad I’m aware enough to recognize this and change my actions.
I love it when students figure stuff out.
I love it even more when:
A. Students figure out things that, as a teacher, I didn’t notice myself.
B. Students who are labeled as “not good at figuring stuff out” figure stuff out.
Here’s what we did today in Algebra 2:
This is a SMILE resource from the National STEM Centre. The problem I thought I would encounter is the word “etc.” Kids don’t do well with “etc.” Etcetera is vague, non-committal, and easily dismissed. To a student, etcetera usually means “I’ll ignore this and see if no one notices.”
It is helpful for me to be more specific with my expectations of students, especially when their mathematical well being is at stake. But today, I was feeling a little vague and non-committal myself, so I handed out the sheet, explained what was going on and let them go…etc.
There are no words I love to hear more in my classroom than “Mrs. Schmidt, look what I figured out.” And today was chock FULL of those statements. Here are a few:
There were lots more. I was very proud of this class’s resolve in addressing the Etcetera.
Nrich has an interesting activity called “Non-transitive Dice” that I’ve always wanted to use in my probability and statistics class. I’m intrigued by the relationship between the strategy in choosing a dice and the probability of winning with that dice.
We don’t have blank dice, so I had my students make their own with cardstock.
Initially, I had them choose which dice would win overall. Then we let the rolling begin: A vs. B, B vs. C, and C vs. A. As they collected their data, they started predicting which dice would end up on top after battle.
Tomorrow, I’d like to sum up the probability representations of some of the dice match-ups. I found this nice post by James Grime (yep, the Numberphile chap) with a few varieties of non-transitive dice. Next year, I might start with his Grime set and have students collect data on different matchups.
If we are successful, hopefully we can workout the probability of these outcomes.
And finally, I know that my students will want to compare this dice game to Rock – Paper – Scissors – Lizard – Spock.
I kept digging into James Grime’s rabbit hole and realized, you can purchase this set of non-transitive dice. Skippy. I might do that!
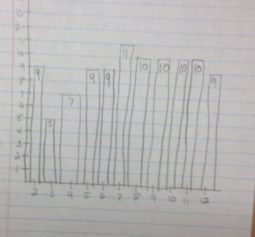
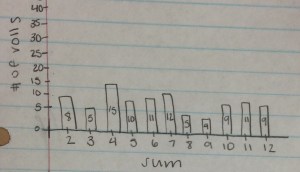
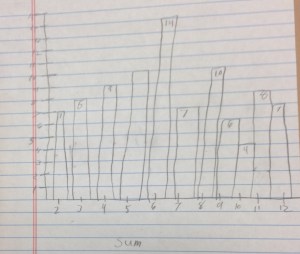
Prompt: You are rolling the dice 99 times and finding the sum on the dice each time. Make a graph showing your prediction of the results.
I’m not sure why every year I think that most of the students will know ahead of time that 6, 7, and 8 come up most often. Of course, the activity is more fun given that they don’t have a clue what’s going to happen.
Uniform
Uniformly Random
Just Random
Peak in Center
I ask the kids if there are any other strategies for their predictions other than the ones we have discussed. One student added that maybe 2 would show up least often and 12 the most, increasing in between. Discussion ensued.
It’s fascinating to me to actually see the students discover what happens and why. I used to have them use the probability simulator on the TI-83/84 but I just don’t trust TI to do anything random anymore. Plus, there’s something more “real” about actually rolling the dice.
They then can compare the graphs of their predictions to their results and discuss differences and reasons for them.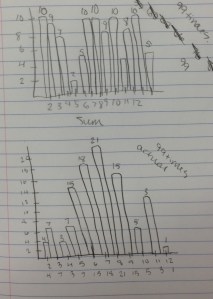 
A question that blew me over today: If we roll two dice over and over, which will happen first – a. rolling a sum of 7, sixteen times, or b. rolling 100 times altogether?
I’m wondering , in a class of 30, what the aggregate results will be on this mystery question.
I realized after searching through my puzzle collection that I possess many of them, but have completed very few. This is true of physical puzzles as well as puzzles on paper. My reasoning: actually doing a puzzle scares the heck out of me because I might not be able to do it. Ironically, I tell people I like puzzles because what crazy person would have a closet full of puzzles in her classroom if she didn’t love them? Fortunately, I make no claims to sanity on this blog, but I’d like to get better at actually attempting puzzles.
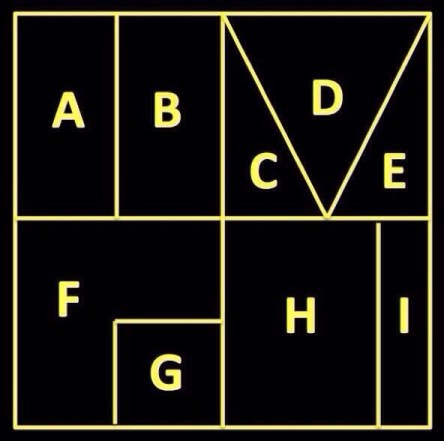
I came across an app called Puzzlium. This app highlights a little bit of all of their great puzzle apps, but the one that caught my eye was Puzzle Quizzes. I was drawn to the short format of these puzzle. It seemed like a good place to start anyway. Here’s an example:
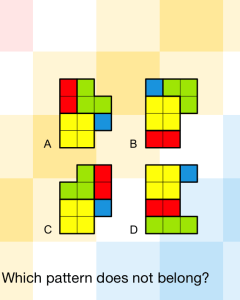
Now, if you’re looking for a place to start in having students “make viable arguments,” this isn’t necessarily an obvious choice. But the simplicity of the question coupled with the inviting color scheme lay down a framework that allows all of them to enter the conversation. I had students who haven’t raised their hand all trimester actively engage in sharing their answers, summarize others, and thoughtfully comment on the arguments of their peers.
This task evolved as the day went on, and my question to my 5th hour class was:
Come up with as many reasons as you can for each of the patterns being the one that does not belong.
Tons of great responses using everything from which colors touched one another to number of blocks in each row/column to perimeter of the total figure. I’ll bet each student in my 5th hour came up with a different argument.
The question that, of course, I wasn’t able to avoid was “So what’s the right answer?” I turned that one right back on them.
“what do you THINK the right answer is? Was there one or more arguments that stood out as “better” than the rest?” The overwhelming response was No. The arguments given were solid and the instructions were ambiguous.
Still, they must know the “right” answer. I made sure to praise their efforts on constructing and presenting their arguments. However, here is the “back of the book” answer:
Showing them this seemed to invite the usual, “ha, I was right and you were wrong” mentality. Maybe next time I’ll resist their pleas and stick with all of them believing they were right.
My brother wisely told me when he saw who I followed on twitter to stop following dumb celebrities and start following some real people. The problem was that back then, I didn’t know which real people to follow. Luckily, I soon discovered that there were math teachers on twitter. Lots of them.
I’ve been to MCTM a couple of times and NCTM once or twice. I felt energized, and motivated after those conferences definitely, but this year was different than any conference I’d previously attended. The difference was my willingness to make a face-to-face connection with people I knew from twitter. I’ve loved twitter for a long time for a variety of reasons, but meeting some tweeps in person and getting to talk math and more math was a real thrill. It mattered less which conference sessions I attended, although they were great, and mattered more who I took the time to interact with in between. Although Christopher Danielson says that he doesn’t remember me as a snarky student in one of his math ed courses, I was grateful to get to spend some quality time talking with the man behind the hierarchy of hexagons. I met many others, and truly got to appreciate the wide range of awesomeness that make up Minnesota’s mathematics teachers.
Next time, though: book a hotel room right away. Lesson learned.
Today my students will have a sub since I am attending our state’s math teacher conference (#mctm). Given the overall success of our Desmos Carnival activity from Monday, I decided that a computer lab activity might be fitting. Since we are starting a unit on probability, I took the opportunity to use some Nrich probability simulations.
I’m also attempting something new with Google Forms. I’ve observed my colleague, Dianna Hazelton, incorporate Google Forms, Sheets, and Docs quite seamlessly into her trigonometry and prob/stat classes. Her success with these apps made me eager to try them out as well. I like that I’m able to “see” what they did via the google form responses right away rather than have a pile of papers waiting for me on Monday.
It’s probability time in my 9th grade prob and stats class. Call me crazy for giving 9th graders dice and pennies with a month left of school, but it’s how I roll. (Ha! I’m cracking up over here!)
I like to start with the Game of Pig, similar to the game used in the IMP curriculum. I adapted it a little to have kids compare strategies for when playing with their own dice (or separate from their partner) to playing with the same dice as their partner.
It’s interesting to see their strategies develop here. Some use very solid ideas like “I stopped when my round score reached 20.” But I also get to see misconceptions like believing that a “one” will be rolled relatively soon after a “two” is rolled. Having them share their strategies helps me to see where these misconceptions lie and deal with them before we start calculating any concrete probability.
Tomorrow, we’ll start by discussing which of these are legitimate strategies and which of them are not.
Number Loving Beagle 
